抱歉，您的浏览器无法访问本站

本页面需要浏览器支持（启用）JavaScript


了解详情 >

七つの海

今日、海を見た。もう怖くない

博客

随笔

朋友

归档

关于

点分治 & 动态点分治 - 学习笔记

七海

算法树上算法

发布于：2020年4月23日

次浏览

开始之前首先是题单：这些题目都是洛谷上的，非常的友好（指访问上）；如果你有什么觉得不错的点分治的题目也可以评论告诉我，我去康康==

点分治
动态点分治
其他补充
  • 弹幕装填中……

因为我很屑，不能保证一次把上边的题目做完，所以需要吊在开头时刻警醒自己==

那么接下来开始本篇文章的正文内容：

背景

点分治是图论中一种树上分治的算法。树分治主要又有两种：点分治和边分治，还有一种以这个为思想的分治树。这里的点分治就是这篇文章要讨论的点分治。

有些题目看起来像是可以使用树上动规，但是却很难使用数组去维护它所需要的信息，这种题目往往需要点分治来解决。通过直接统计或者加上数据结构维护，就可以统计之前不好统计一些的东西。

顾名思义，点分治是一种分治，还是在点上的分治。每次把无根树拆成子树，递归进行处理，最后通过计算贡献的方式将计算结果合并，得到最终整个树的答案。

点分治

刚才也说了，点分治是分治，需要递归的处理子树。事实上代码里也是成块成块的DFS。显然，这样的递归的时间受到它最大的子树的大小的影响：比如极端情况下，链的递归时间复杂度是O(n²)。但是比起一般的搜索，点分治在拆分之前会优先寻找无根树的重心，将它作为根进行递归。

树的重心： 以重心为此无根树的根，这棵树的最大子树最小。若全树的大小为n，以重心为根时的每一个子树的大小都不超过n/2（可使用反证法证明）。

如果每次递归都是寻找树的重心进行，那么递归层数一定是最优的。所以本质上，点分治是优化的暴力，在合并过程还会用到容斥原理的思想。点分治每次递归都选择重心作为分治点，问题规模上界降低到原来的1/2，使得整体的复杂度降低到O(nlogn)。

接下来通过解最经典的点分治的题目洛谷 P4178 Tree，来详细说明点分治的每一个过程。建议看下面的内容之前先去读个题，或者拉到后面看完这个题的题解。

求树的重心

知道了重心好，那么怎么找到这个最优的分治点呢？暴力找：DFS的话可以在O(n)的时间里找到。findRoot函数可以找到一颗无根树的重心，将无根树转化为有根树，利用递归统计子树大小。这里的代码和后面的代码都使用了前向星存树，使用了FWS的一些经典变量：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
int findRoot(int u, int father)
{
    size[u] = 1; int maxPart = 0;
    for (int c = head[u]; ~c; c = ee[c].next)
    {
        edge& e = ee[c]; int& v = e.v;
        if (v == father || vis[v]) continue;
        findRoot(v, u);
        size[u] += size[v];             
        maxPart = max(maxPart, size[v]);
    }
    maxPart = max(maxPart, _sum - size[u]);
    if (maxPart < _part) setRoot(u, maxPart);
    return _root;
}

上面的函数中：size[u]表示以u在当前递归的顺序下作为根节点的子树的大小（节点数量）；maxPart用来记录当前已经找到的最大子树；_sum保存了当前查找重心的全树的大小；_part和_root用来暂存结果：重心节点的编号和它的max-part，使用宏setRoot更新。

因为整个树是无根树，所以子树大小也只是“当前递归的顺序下作为根节点”意义上的。也就是说，虽然这个点可能是被递归调用的，father是有意义的节点；但是因为是无根树，节点u的“当前递归的顺序下“的父节点以及其他兄弟节点，也可以被看作u的一颗子树——这棵子树的大小就使用容斥原理进行计算：sum - size[u]。

显然，你的顶层调用（非递归调用）是为了寻找一整颗树的重心：你需要将_sum初始化为这棵树的大小、_part初始化为无穷大、_root初始化为不存在的节点，然后才能开始搜索。我写了宏cleanRoot来完成这项工作。

从重心开始分治

我们知道了重心，那么就可以以重心作为分治点开始分治递归了。虽然具体的分治函数要取决于问你的模型，但是分治函数具有相似的特点。对于这个题目，我们做出的分治是：对于每颗树，只考虑经过它的根的路径；其他的路径因为一定会经过子树的根，所以作为子问题分治。

这里贴的代码仅针对这道题目：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
void dc(int u)
{
    ans += process(u, 0);	////////////////////////
    vis[u] = true;
    for (int c = head[u]; ~c; c = ee[c].next)		
    {
        edge &e = ee[c]; int &v = e.v;
        if (vis[v]) continue;
        ans -= process(v, e.w);	////////////////////
        cleanRoot(size[v]);
        auto root = findRoot(v, u);
        dc(root);
    }
}

两行用斜杠标记的部分是本题特殊的地方；一般的核心分治函数的大概结构就像上面这样。process是本题中用来计算答案的函数；宏cleanRoot用来重置root信息。

对于本题，process函数可以求出当前树中所有子节点到根节点的距离。我们先看它出现的两行：第一次出现不难理解，要求出经过根节点的路径，必然要先求出这些”半路径“进行组合；但是第二次出现却显得有些莫名其妙。

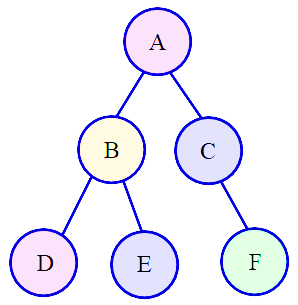
首先我们考虑下面的树：

1126418-20180317225729674-1956875804.png

第一行的process会求出这些半边："A"、"A - B"、"A - B - D"、"A - B - E"、"A - C"、"A - C - F"——准确的说是将它们的长度可重复的存进数组。根据分析，接下来只要将它们俩俩组合，就可以得到分析的”通过树根的路径“。但是显然，"A - B - D"、"A - B - E"组合得到的"D - B - A - B - E"并不是一条合法路径。

究其原因，是因为参加组成的两条”半边“都来自于A的同一颗子树B。所以，最直接的方法，就是对于每颗子树单独统计来自它的到根的边的贡献，将它们从答案中减去。因为此时求的仍然是到根A的距离，但是DFS从B开始，所以统计得到到B的长度都应该加上"A - B"的边长。

这样利用容斥原理，最终在这次分治中对答案造成的贡献，就是分析中要求的”经过根节点的路径“。对于这个节点，总的时间复杂度是O(nlogn)。非常好。

那么接下来的分治的时间复杂度要怎么保证呢？这个时候，应该再次意识到这是一颗无根树——将一个节点算完之后，它的子树之间就互不影响了。对于它的每颗子树，我们都可以当作一个新问题——找到重心保证最优递归深度，然后继续分治。又因为重心的子树的大小不超过全树的一半，每次寻找重心的递归深度上界是logn，因此整体复杂度是O(nlog²n)。

能看到上面的代码的后半部分就是：首先重置并且寻找子树的重心，然后对子树启动分治。

子树找重心

因为子树完全和全树是同样的问题，所以可以采用同样的流水线：先初始化root，再从子树的”第一个端点“——也就是直接和上一轮的重心相连的节点开始找到重心，然后启动分治。

这里有一个问题：最开始，对于全树而言，_sum = n并没有什么问题。但是对于子树来说，_sum == size[u]真的成立吗？因为是无根树，子树中直接连接上轮重心的节点未必是本轮这颗子树的重心：这导致本轮处理的传入的树的总点数可能并不正确。我先列出正确的式子：

1
2
-	_sum = size[v];
+ 	_sum = size[v] > size[u] ? _sum - size[u] : size[v]

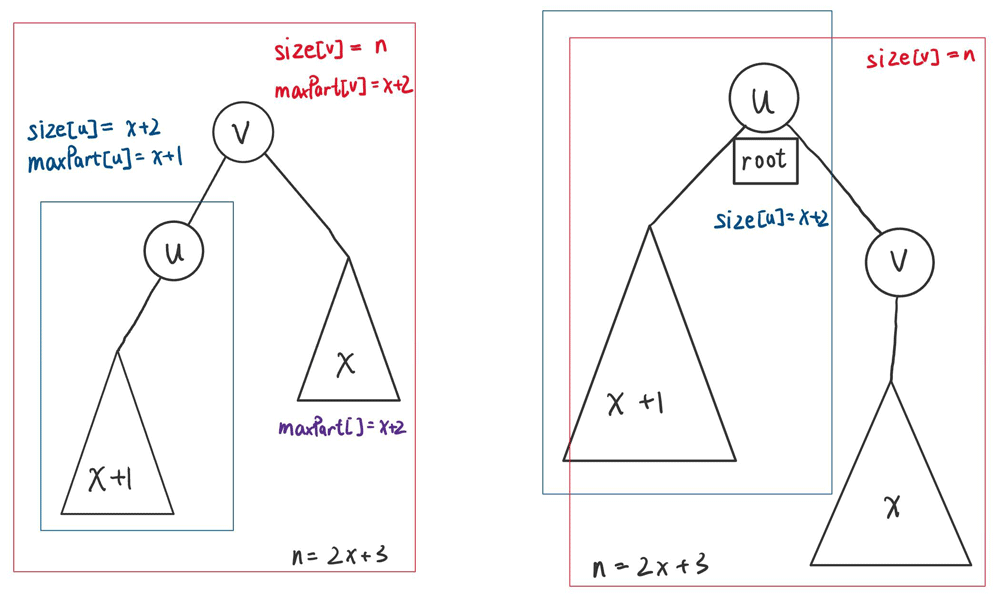
要想知道之前设置为size[v]对不对，我们首先要知道size是怎么来的：这里传入的size[v]，准确的定义是”本轮中与上一轮的重心相连的点，以上轮的根为根（父节点）的子树大小“。因为是无根树，我们已经知道了”根“可能并不是”重心“，于是就有可能出现下图所示的情况：

RYH4YJ_5YN_XTMNHS2TD80K.png

上一轮的根为v，重心为u：此时若对重心u的子树v进行寻根，很显然size[v]并不是子树的大小。当本轮的根（起始搜索点）和上轮的根在上轮的重心的同一颗子树中的时候，size[v]是错误的值，应当修正。

但是这个错误真的影响这个算法的复杂度或正确性吗？我们先回顾一下我们的寻找重心的方式：从本轮的”根“开始DFS，并且计算子树大小；将传入的全树大小与以自身为根的子树大小的差作为”根方向“的子树的大小，从而计算最大子树的大小。

结论是不影响的，所以大可不必写麻烦的代码。数学证明可以去看这篇文章：传送门

算法流程

总结一下上面的内容，可知针对于无根树的点分治算法一共分为三步：

  • 找到当前全树的重心，并以该重心作为分治点
  • 启动分治，并且调用解题/计算函数处理当前树的整体
  • 找到每一颗子树的重心，作为子问题发起新的分治

难点就在解题/计算函数的设计。一般而言，点分治适合处理树上简单路径的问题，但是也不止于此。很多题目通过巧妙的构造计算函数，也可以使用点分治快速解决。至于分治的设计：处理树上简单路径的时候，往往将树上的路径分为经过当前分治点的和不经过分治点的两种类型：第一类在本次分治时使用其他函数处理，第二类作为子问题递归处理。

动态点分治

刷题记录

这里刷题的顺序可能和上面的题单顺序不一样，请明察（

洛谷 P4178 Tree

文　明　起　源（大雾； 这里只介绍点分治做法

给定一颗n个节点的有边权树，求树上两点距离小于等于k的点对数量。

数据规模：N = 4e4，边权小于1000，K = 2e4

虽然上面讲点分治已经非常仔细的介绍了，这里就简单的进行一下分析：

显然这个题目没办法用简单的DFS来统计——那应该怎么在DFS中统计树中符合条件的路径数量？一般的DFS对于这种树上路径统计的问题是苦手的。

假设我们已经找到了全树重心root。对于全树中的路径，我们把它分为两类：第一类经过了root，另一类没经过。显然，后者一定完全在t的某棵子树里面，而前者不在。也就是说，答案 = 经过root的路径的答案 + root的所有子树的子问题的答案；对于子问题，直接递归，只需要考虑第一类答案即可。

第一类答案是通过根节点的路径长度。这种长度显然可以拆成两条从根节点出发的简单路径的长度和，然而从根节点出发的简单路径的长度是很容易DFS得到的。对于一棵树，可以将从根节点出发得到的所有路径长度存进数组里，然后将它们两两匹配，就可以得到第一类路径。

这里还存在隐含的问题：若两条简单路径来自于根的同一颗子树，则它们组成的路径含有重边，是无效的；对于这种情况，我们依然可以利用容斥思想：仅统计子树中的节点到根的简单路径，将这些简单路径的贡献从答案中剔除，剩下的就都是来自不同子树的简单路径的贡献了。

统计完一棵树中所有路径长度之后，可以利用双指针的策略来获得所有满足要求的匹配的数量。至此，我们知道这样的实现步骤：

  • DC主操作：统计全树合法匹配，对每一棵子树利用容斥减去来自同子树的贡献
  • 计算函数：DFS计算全树所有节点到根的距离，并且存入特定数组
  • 统计函数：利用双指针的技巧，统计出计算函数求出的路径的合法对数，并返回DC主操作

这样，就可以修改模板解出这个题目了。具体实现请看下面的全部代码。

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
#include <iostream>
#include <cstring>
#include <algorithm>

using namespace std;
using longs = long long;

const int inf = 0x3f3f3f3f;

struct edge
{
    int u, v, w, next;
    edge() = default;
    edge(int u, int v, int w, int next)
            : u(u), v(v), w(w), next(next) {}
};

const int N = 4e4+5, M = N;
int n, k, ans = 0;

namespace FWS
{
    int head[N];
    int tot;
    edge ee[M * 2];

    void init()
    {
        memset(head, -1, sizeof(int)*(n+1));
        tot = 0;
    }

    void addedge(int u, int v, int w)
    {
        ee[tot] = edge(u,v,w,head[u]);
        head[u] = tot ++;
    }
}

namespace PointDC
{
    int size[N];            // size统计整个子树大小
    bool vis[N];            // 记录子树是否已经被分治处理过
    int _sum;               // 记录将要分治的子树大小，以计算另一个子树的大小
    int _root;              // findRoot中用来临时记录找到的重心
    int _part;              // findRoot当前找到的重心的maxPart

    int path[N], cnt = 0;

    void(*calculate)(int,int,int) = [](int u, int father, int distance)
    {
        path[cnt ++] = distance;
        using namespace FWS;
        for (int c = head[u]; ~c; c = ee[c].next)
        {
            edge& e = ee[c]; int& v = e.v;
            if (v == father || vis[v]) continue;
            calculate(v, u, distance + e.w);
        }
    };

    auto cleanRoot = [](int size)
    {
        _root = 0; _part = inf;
        _sum = size;
    };

    auto setRoot = [](int u, int maxPart)
    {
        _part = maxPart;
        _root = u;
    };

    inline void init()
    {
        memset(vis, 0, sizeof(bool) * (n + 1));
        setRoot(0, inf);
    }

    int findRoot(int u, int father)
    {
        size[u] = 1; int maxPart = 0;
        using namespace FWS;
        for (int c = head[u]; ~c; c = ee[c].next)
        {
            edge& e = ee[c]; int& v = e.v;
            if (v == father || vis[v]) continue;
            findRoot(v, u);
            size[u] += size[v];             // 统计子树大小，以找到最大子树
            maxPart = max(maxPart, size[v]);
        }
        maxPart = max(maxPart, _sum - size[u]);
        if (maxPart < _part) setRoot(u, maxPart);
        return _root;
    }

    int process(int u, int distance)        // 双指针做法
    {
        cnt = 0; calculate(u, 0, distance);
        int _ans = 0, l = 0, r = cnt - 1;
        sort(path, path + cnt);
        for (;; ++l)
        {
            while (r != -1 && path[l] + path[r] > k) -- r;
            if (r < l) break;
            _ans += r - l + 1;				// 这个区间都可以和l配对
        }
        return _ans;
    }

    void dc(int u)
    {
        ans += process(u, 0);
        vis[u] = true;
        using namespace FWS;
        for (int c = head[u]; ~c; c = ee[c].next)
        {
            edge &e = ee[c]; int &v = e.v;
            if (vis[v]) continue;
            ans -= process(v, e.w);			// 只需要来自不同子树的配对
            cleanRoot(size[v]);
            auto root = findRoot(v, u);
            dc(root);
        }
    }

    void solution()
    {
        init();
        cleanRoot(n);
        auto root = findRoot(1, 0);
        dc(root);
    }
}

int main()
{
    ios::sync_with_stdio(false);
    cin.tie(nullptr);

    auto addEdge = [&](int u, int v, int w)
    {
        FWS::addedge(u, v, w);
        FWS::addedge(v, u, w);
    };

    // freopen(R"(D:\shiroha\Downloads\P4178_1.in)", "r", stdin);

    cin >> n; int u, v, w;
    FWS::init();
    for (int i = 1; i < n; ++ i)
    {
        cin >> u >> v >> w;
        addEdge(u, v, w);
    }
    cin >> k;
    PointDC::solution();
    cout << ans - n << endl;        // 答案不包括单点

    return 0;
}

这个题目似乎还有其他的解法，但是这里就不赘述了。

洛谷 P3806 【模板】点分治1

我做的第一个点分治的题目（毕竟是模板

给定一颗 n 个节点的有边权树，询问树上距离为 k 的点对是否存在，询问 m 次。

N = 1e4，M ≤ 100，边权小于1e4，K = 1e7

和上一个题非常相似，只不过询问的东西变成了是否等于 k，并且询问的次数变多了。

每询问一次就找一次显然不太合算，反正题目也没有要求强制在线，可以一次读入所有的请求，然后离线处理所有的答案，最后统一输出。

和上一题一样，这一题也可以用一个DFS将全树/某一子树所有可能出现的到根节点的距离求出来。但是这一次如果像上一题那样求出所有的和，想必是不太划算的。为判断长度为k的边是否存在，每次扫完一颗子树之后，就求出询问长度对这次求出的路径长度的差，并记录。之后如果扫描到的长度恰好存在相等的”差“的记录，就说明它一定可以和之前子树中出现的某条路径组合成满足要求长度的边。

这是一种比较巧妙的做法：不仅避免了两条路径同源的问题，还避免了求出所有的路径和查找。记录这些”差“，可以采用访问是O(1)的桶。

注意到题目中说到询问的最大值是K，那么就可以使用K作为桶的大小：不论是超过K的边还是超过K的”差“的记录，一定不会对答案造成贡献，可以直接忽视。事实上，内存限制也不允许我们开太大的桶。

代码

其实这才是我做的最早的一个点分治的题目，有些风格和现在的不一样。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
#include <iostream>
#include <algorithm>
#include <cstring>
#include <functional>

using namespace std;

struct edge
{
    int u, v, w, next;
    edge() = default;
    edge(int u, int v, int w, int next)
            : u(u), v(v), w(w), next(next) {}
};

const int N = 10010, M = N;
const int INF = 0x3f3f3f3f;

int n, m, queries[105];

namespace FWS
{
    int head[N];
    int tot;
    edge ee[M*2];

    void init()
    {
        memset(head, -1, sizeof(int)*(n+1));
        tot = 0;
    }

    void addedge(int u, int v, int w)
    {
        ee[tot] = edge(u,v,w,head[u]);
        head[u] = tot ++;
        ee[tot] = edge(v,u,w,head[v]);
        head[v] = tot ++;
    }
}

namespace PointDC
{
    int maxPart[N];         // subtree记录最大子树
    int size[N];            // size统计整个子树大小
    bool vis[N];            // 记录子树是否已经被分治处理过
    int sum;                // 记录将要分治的子树大小，以计算另一个子树的大小
    int _root;              // findRoot中用来临时记录找到的重心

    const int buf = 1e7;    // 标记距离的桶大小：询问的上限
    bool has[buf+5];        // 到根距离为i的路径是否存在
    int rem[N];             // 记录全树中可能出现的路径长度；[0]记录实际长度
    int dis[N];             // 记录节点到子树根的距离
    int can[N];             // calculate中，和cnt一起用来临时记录出现过的距离
    int* _query;            // 离线算法：记录的询问
    int _count;             // 离线算法：询问的数量
    bool test[N];           // 离线算法：用来标记i号询问的结果

    inline void init()
    {
        memset(vis, 0, sizeof(bool) * (n + 1));
        memset(has, 0, sizeof(bool) * (n + 1));
        memset(test, 0, sizeof(bool) * (n + 1));
        _query = ::queries;
        _count = ::m;
        _root = 0;
        rem[0] = 0;
    }

    int findRoot(int u, int father)
    {
        size[u] = 1; maxPart[u] = 0;
        using FWS::head; using FWS::ee;
        for (int c = head[u]; ~c; c = ee[c].next)
        {
            edge& e = ee[c]; int& v = e.v;
            if (v == father || vis[v]) continue;
            findRoot(v, u);
            size[u] += size[v];             // 统计子树大小，以找到最大子树
            maxPart[u] = max(maxPart[u], size[v]);
        }
        maxPart[u] = max(maxPart[u], sum - size[u]);
        if (maxPart[u] < maxPart[_root])
            return _root = u;
        else return _root;
    }

    void distance(int u, int father)
    {
        rem[++rem[0]] = dis[u];             // 标记当前树根的距离
        using FWS::head; using FWS::ee;
        for (int c = head[u]; ~c; c = ee[c].next)
        {
            edge &e = ee[c]; int &v = e.v;
            if (v == father || vis[v]) continue;
            dis[v] = dis[u] + e.w;
            distance(v, u);                 // 递归地查找子树
        }
    }

    void calculate(int u)
    {
        int cnt = 0;
        using FWS::head; using FWS::ee;
        for (int c = head[u]; ~c; c = ee[c].next)
        {
            edge& e = ee[c]; int& v = e.v;
            if (vis[v]) continue;
            rem[0] = 0; dis[v] = e.w;
            distance(v, u);                 // 计算该子树中点到顶点u的距离
            for (int j = rem[0]; j; --j)    // rem记录了该子树所有点到u距离
                for (int k = 1; k <= _count; ++ k)
                    if (_query[k] >= rem[j])
                        test[k] |= has[_query[k] - rem[j]];
            for (int j = rem[0]; j; --j)
            {
                if (rem[j] > buf) continue; // 针对：超出询问范围，忽略
                can[++cnt] = rem[j];
                has[rem[j]] = true;
            }
        }
        for (int i = 1; i <= cnt; ++ i)     // 处理完子树后，清空标记
            has[can[i]] = false;
    }

    void dc(int u)
    {
        vis[u] = has[0] = true;
        calculate(u);                       // 查找子树u中的“第一类路径”
        using FWS::head; using FWS::ee;
        for (int c = head[u]; ~c; c = ee[c].next)
        {
            edge& e = ee[c]; int& v = e.v;
            if (vis[v]) continue;
            sum = size[v];                  // 顶层查找子树重心调用
            maxPart[_root = 0] = ::INF;
            int root = findRoot(v, 0);
            dc(root);                       // 分治：进而处理子树
        }
    }

    void solution()
    {
        init();
        maxPart[_root] = sum = n;          // 初始化：查找全树重心
        int root = findRoot(1, 0);
        dc(root);                           // 开始分治
    }
}

int main()
{
    ios::sync_with_stdio(false);
    cin.tie(nullptr);

//    freopen(R"(D:\shiroha\Downloads\P3806_7.in)","r",stdin);

    int u, v, w;
    cin >> n >> m;
    FWS::init();
    for (int i = 1; i < n; ++ i)
    {
        cin >> u >> v >> w;
        FWS::addedge(u,v,w);
    }
    for (int i = 1; i <= m; ++ i)
        cin >> queries[i];
    PointDC::solution();

    for (int i = 1; i <= m; ++ i)
        cout << (PointDC::test[i] ?
                 "AYE" : "NAY")
             << endl;
    return 0;
}

注释还算比较详细吧，我觉得光看代码应该就很好懂了。

洛谷 P2634 [国家集训队]聪聪可可

实际上这题的最优复杂度是树上DP，可以O(n)解出来。

给一个有n个节点的带边权树，问树上长度可以被3整除的路径数量和全部树上路径数量的比值，并以约分后的分数的形式输出答案。

数据范围：N = 2e4

和前面几个题不一样，本题统计的是树上路径长度可以被3整除的路径数量。我们可以参考上面题目的做法：将树上路径分成两类——其中第一类路径可以通过两个不同源的”半边“组合得到。因为模3的余数只有三种情况，得到长度可以被3整除的路径只有两种情况：余0和余0组合或者余1和余2组合。我们可以统计当前子树中到根距离模3分别为0、1、2的路径数量，按照上述规则进行组合，得到第一类路径的数量。

因为组合路径不能同源，可以使用和上面第一题一样的容斥原理分别排除子树的同源贡献。因为我们只考虑对于3的模，所以读入边权时就取模，可以避免可能会出现的边权爆int的情况。

求出了全树中，路径长度模3为0的数量之后，意识到全树的边的数量就是n*n。然后求出总边数和符合要求的路径数量的gcd，约去后输出就是答案。

代码

因为这是讲点分治的文章，树形DP做法就不贴了。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
#include <iostream>
#include <cstring>
#include <algorithm>

using namespace std;

const int inf = 0x3f3f3f3f;

struct edge
{
    int u, v, w, next;
    edge() = default;
    edge(int u, int v, int w, int next)
            : u(u), v(v), w(w), next(next) {}
};

const int N = 4e4+5, M = N;
int n, ans = 0, cnt[3], dis[N];

namespace FWS
{
    int head[N];
    int tot;
    edge ee[M * 2];

    void init()
    {
        memset(head, -1, sizeof(int)*(n+1));
        tot = 0;
    }

    void addedge(int u, int v, int w)
    {
        ee[tot] = edge(u,v,w,head[u]);
        head[u] = tot ++;
    }
}

void addEdge(int u, int v, int w)
{
    FWS::addedge(u, v, w);
    FWS::addedge(v, u, w);
}

namespace PointDC
{
    int size[N];            // size统计整个子树大小
    bool vis[N];            // 记录子树是否已经被分治处理过
    int _sum;               // 记录将要分治的子树大小，以计算另一个子树的大小
    int _root;              // findRoot中用来临时记录找到的重心
    int _part;              // findRoot当前找到的重心的maxPart

    using dfs = void(*)(int, int);

    dfs search = [](int u, int father)
    {
        ++ cnt[dis[u]];
        using namespace FWS;
        for (int c = head[u]; ~c; c = ee[c].next)
        {
            edge& e = ee[c]; int& v = e.v;
            if (v == father || vis[v]) continue;
            dis[v] = (dis[u] + e.w) % 3;
            search(v, u);
        }
    };

    auto cleanRoot = [](int size)
    {
        _root = 0; _part = inf;
        _sum = size;
    };

    auto setRoot = [](int u, int maxPart)
    {
        _part = maxPart;
        _root = u;
    };

    inline void init()
    {
        memset(vis, 0, sizeof(bool) * (n + 1));
        setRoot(0, inf);
    }

    int findRoot(int u, int father)
    {
        size[u] = 1; int maxPart = 0;
        using namespace FWS;
        for (int c = head[u]; ~c; c = ee[c].next)
        {
            edge& e = ee[c]; int& v = e.v;
            if (v == father || vis[v]) continue;
            findRoot(v, u);
            size[u] += size[v];
            maxPart = max(maxPart, size[v]);
        }
        maxPart = max(maxPart, _sum - size[u]);
        if (maxPart < _part) setRoot(u, maxPart);
        return _root;
    }

    int calculate(int u, int distance)
    {
        memset(cnt, 0, sizeof cnt);
        dis[u] = distance;
        search(u, 0);
        return cnt[0] * cnt[0] + cnt[1] * cnt[2] * 2;
    }

    void dc(int u)
    {
        ans += calculate(u, 0);
        vis[u] = true;
        using namespace FWS;
        for (int c = head[u]; ~c; c = ee[c].next)
        {
            edge &e = ee[c]; int &v = e.v;
            if (vis[v]) continue;
            ans -= calculate(v, e.w);
            cleanRoot(size[v]);
            auto root = findRoot(v, u);
            dc(root);
        }
    }

    void solution()
    {
        init();
        cleanRoot(n);
        auto root = findRoot(1, 0);
        dc(root);
    }
}

int gcd(int a,int b)
{
    return b == 0 ? a : gcd(b, a % b);
}

int main()
{
    ios::sync_with_stdio(false);
    cin.tie(nullptr);

    cin >> n; FWS::init();
    for (int i = 1; i < n; ++ i)
    {
        int u, v, w;
        cin >> u >> v >> w;
        addEdge(u, v, w % 3);
    }
    PointDC::solution();
    cerr << ans << endl;
    int tot = n * n,
        xx = gcd(tot, ans);
    cout << (ans / xx) << '/' << (tot / xx) << endl;

    return 0;
}

和万物起源Tree一样，统计长度模3不同余数的路径数量再组装成”第一类路径“，递归处理”第二类路径“。

洛谷 P4149 [IOI2011]Race

题面言简意赅

给一棵树，每条边有权。求一条简单路径，权值和等于k，且边的数量最小；点从0开始编号；若不存在这样的路径，输出-1；否则，输出这样的路径包含的边数。

数据范围：N = 2e5，K = 1e6，边权不超过K。

这题要是用树形DP：设 f[i][j] 是以i为根的子树中长度为j的路径最小边数，那光是空间复杂度就已经是 N*K 的爆炸水准了，更不必说还要手动转移填满它的时间；所以使用点分治来做：

和前面求等于k的书上路径一样：使用桶存储之前开的子树中找到的长度，并且使用另一个桶维护每一种路径长度在已经搜索过的子树中出现的最少边数。在查找子树的过程中，利用当前的边的长度和桶维护的信息更新答案的最小值即可；用树规一点的说法，就是 f[j] 表示以重心为根的子树中长度为j的路径最小边数：在分治点DFS更新该数组，并顺便使用和为k的第一类路径去更新ans即可。

综上所述：使用点分治解决此题，空间复杂度是 O(K)，时间复杂度 O(nlogn)。

需要注意的是：因为询问有上限K，所以桶开到K就可以了；此外，当前搜索过程中距离已经大于k的情况，可以直接剪枝返回。

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
#include <iostream>
#include <cstring>
#include <algorithm>

using namespace std;
using longs = long long;

const int inf = 0x3f3f3f3f;
const longs INF = 0x3f3f3f3f3f3f3f3f;

struct edge
{
    int u, v, w, next;
    edge() = default;
    edge(int u, int v, int w, int next)
            : u(u), v(v), w(w), next(next) {}
};

const int N = 2e5+5, M = N;
int n, k, ans = inf;
longs dis[N];

namespace FWS
{
    int head[N];
    int tot;
    edge ee[M * 2];

    void init()
    {
        memset(head, -1, sizeof(int)*(n+1));
        tot = 0;
    }

    void addedge(int u, int v, int w)
    {
        ee[tot] = edge(u,v,w,head[u]);
        head[u] = tot ++;
    }
}

void addEdge(int u, int v, int w)
{
    FWS::addedge(u, v, w);
    FWS::addedge(v, u, w);
}

namespace PointDC
{
    int size[N];
    bool vis[N];
    int _sum;
    int _root;
    int _part;

    using dfs = void(*)(int, int);

    const int buf = 1e6 + 5;
    int rem[N], path[N], cnt = 0;
    int len[buf], _now;
    int used[buf], has[buf];

    dfs distance = [](int u, int father)
    {
        int nowPath = _now + 1;
        if (dis[u] <= k)
        {
            ans = min(ans, nowPath + len[k - dis[u]]);
            rem[++ cnt] = dis[u];
            path[cnt] = nowPath;
        }
        else return;
        using namespace FWS;
        for (int c = head[u]; ~c; c = ee[c].next)
        {
            edge &e = ee[c]; const int v = e.v;
            if (vis[v] || v == father) continue;
            dis[v] = dis[u] + e.w;
            _now = nowPath; distance(v, u);
        }
    };

    auto cleanRoot = [](int size)
    {
        _root = 0; _part = inf;
        _sum = size;
    };

    auto setRoot = [](int u, int maxPart)
    {
        _part = maxPart;
        _root = u;
    };

    inline void init()
    {
        memset(vis, 0, sizeof(bool) * (n + 1));
        memset(len, 0x3f, sizeof(len));
        memset(has, 0, sizeof(has));
        len[0] = 0;
        setRoot(0, inf);
    }

    int findRoot(int u, int father)
    {
        size[u] = 1; int maxPart = 0;
        using namespace FWS;
        for (int c = head[u]; ~c; c = ee[c].next)
        {
            edge& e = ee[c]; int& v = e.v;
            if (v == father || vis[v]) continue;
            findRoot(v, u);
            size[u] += size[v];
            maxPart = max(maxPart, size[v]);
        }
        maxPart = max(maxPart, _sum - size[u]);
        if (maxPart < _part) setRoot(u, maxPart);
        return _root;
    }

    void calculate(int u)
    {
        dis[u] = used[0] = 0;
        using namespace FWS;
        for (int c = head[u]; ~c; c = ee[c].next)
        {
            edge &e = ee[c]; const int v = e.v;
            if (vis[v]) continue;
            dis[v] = e.w; cnt = _now = 0;
            distance(v, u);
            for (int j = cnt; j; -- j)
            {
                if (!has[rem[j]])
                {
                    used[++ used[0]] = rem[j];
                    has[rem[j]] = true;
                }
                len[rem[j]] = min(len[rem[j]], path[j]);
            }
        }
        for (int i = used[0]; i; -- i)
        {
            len[used[i]] = inf;
            has[used[i]] = false;
        }
    }

    void dc(int u)
    {
        vis[u] = true; calculate(u);
        using namespace FWS;
        for (int c = head[u]; ~c; c = ee[c].next)
        {
            edge &e = ee[c]; int &v = e.v;
            if (vis[v]) continue;
            cleanRoot(size[v]);
            auto root = findRoot(v, u);
            dc(root);
        }
    }

    inline void solution()
    {
        init();
        cleanRoot(n);
        auto root = findRoot(0, 0);
        dc(root);
    }
}

int main()
{
    ios::sync_with_stdio(false);
    cin.tie(nullptr);

//    freopen(R"(D:\shiroha\Downloads\P4149_2.in)", "r", stdin);

    cin >> n >> k; FWS::init();
    for (int i = 1; i < n; ++ i)
    {
        int u, v, w;
        cin >> u >> v >> w;
        addEdge(u, v, w);
    }
    PointDC::solution();
    cout << (ans >= inf ? -1 : ans) << endl;

    return 0;
}

基本还是套板子：只是注意到顶点从0开始，需要修改PointDC::solution里查找重心的起点。

洛谷 P2664 树上游戏

和上面的裸的树上路径长度不同，这题就麻烦一些了：

一颗有 n 个节点的无边权树，每个节点有一个标号为 ci 的颜色；定义 s(i, j) 是树上路径 i - j 上出现的不同颜色种数；此外定义 sum(i) ： \[ sum(i) = \sum_{j = 1}^n s(i, j) \] 求出这棵树的所有 sum(i)；数据范围：N = 1e5.

虽然，这种数据规模可以接受 nlogn，处理树上点对且单次询问的问题，一定是点分治；使用点分治通常的分治方法，问题集中到如何使用 O(n) 时间处理子树中“第一类路径”对答案的贡献。

对于树上的分治点：我们可以统计从它出发可到达的所有节点和它自身之间形成的路径对答案的贡献，也可以统计经过它的路径对于路径端点的贡献；两种都是属于第一类路径；对自己的贡献比较好统计，dfs的时候加和就行；接下来考虑如何统计第二类的贡献。

先说一个显而易见的结论：对于树中节点 i，若它的颜色在从它到当前树根（分治点）的路径中第一次出现，那么所有和 i 的LCA为根的节点（也就是根节点以及根节点的其他子树的节点）都可以和 i 的子树中的节点 j 形成“第一类路径”；在不考虑其他子树中出现相同颜色的情况下，i 的颜色会对这些点的答案产生 size[i] 的贡献（size[i] 条不同的路径，每条路径贡献1个颜色点）。

上面的内容也可以这么说：因为要求的是全部路径（所有点对），所以显然要考虑贡献；我们先考虑“半边”第一类路径，也就是从根出发到子树中的点组成的点对：那么如果点 i 的颜色在根到 i 中第一次出现，那么 i 和 i 的子树中所有点都会因为这个颜色而导致 s 值加 1——这一点贡献是 i 的颜色带来的。

然后就是遍历子树，分子树考虑：首先采用同样的DFS将当前子树的颜色的贡献从总贡献中减去；然后考虑这颗子树中的一个点，令这个点到当前根上的路径中的不同颜色数是colors，other表示当前树出了该子树之外的其他部分的点数，X是这个点到根的路径上不包括根的颜色的贡献之和；对于这些已经出现过的颜色，在它们作为子树根的时候必然已经考虑过了，所以先从总贡献中减去；这样就可以考虑对于子树节点的贡献了。

简单的说，在某点作为分治点时，统计了从它出发到它的所有子节点形成的“半边”对自己的sum产生的贡献：因为根的颜色的贡献只能是自己产生，所以要剪掉这个颜色的贡献，加上因为自己拥有这个颜色而导致的这个颜色的贡献加成size[u]；接下来，要考虑所有的子树的根出发向上经过本分治点对这些子树的根节点产生的贡献——半边已经确定，就是分治点到子树根的链上的颜色，另半边的颜色贡献已经使用total维护，当然，这里要减去那个已经确定的半边上有的颜色带来的贡献。这样，分治点的“第一类路径”就处理完了。

应当注意的是，sum只考虑起点和终点，并不考虑经过的点：这和分治的“第一类路径”的定义不太一致；这里主要是将每一个点的“第一类路径”分成对分治点下探对自身的影响和对于子树节点上探的影响。

综上所述，我们可以在每一层分治的分治点这么做：

  • 执行DFS.count：统计转化为以分治点为根的有根树的各子树的大小，并统计上面结论里说的贡献（记录到contrib数组），以及这些贡献的和（total）；
  • 考虑分治点下探对分治点带来的贡献：total - contrib[.c] + size
  • 枚举子树，考虑子树节点上探经过分治点带来的贡献：
    • 执行DFS.disContrib，消除当前子树自身对颜色带来的贡献；
    • 执行DFS.update，加算贡献更新子树节点的答案；
    • 执行DFS.reContrib，回复第一步扣除的子树影响，为其他子树所用；
  • 清空颜色贡献数组：本层分治处理完成，返回dc进行下一步的分治

如果你还是觉得上面说的不太清楚，可以看看下面的代码。

代码

这里贴出的是使用点分治在 O(nlogn) 的时间内解决的代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
242
243
244
245
246
247
248
249
250
251
252
253
254
255
256
257
258
#include <iostream>
#include <cstring>
#include <algorithm>

using namespace std;
using longs = long long;

const int inf = 0x3f3f3f3f;

struct edge
{
    int u, v, w, next;
    edge() = default;
    edge(int u, int v, int w, int next)
            : u(u), v(v), w(w), next(next) {}
};

const int N = 1e5+5, M = N;
int n, c[N];
longs sum[N];

namespace FWS
{
    int head[N];
    int tot;
    edge ee[M * 2];

    void init()
    {
        memset(head, -1, sizeof(int)*(n+1));
        tot = 0;
    }

    void addedge(int u, int v, int w)
    {
        ee[tot] = edge(u,v,w,head[u]);
        head[u] = tot ++;
    }
}

void addEdge(int u, int v, int w)
{
    FWS::addedge(u, v, w);
    FWS::addedge(v, u, w);
}

namespace PointDC
{
    int size[N];
    bool vis[N];
    int _sum, _root, _part;

    namespace innerDFS
    {
        using dfs = void(*)(int, int);

        longs contrib[N];
        longs total;
        int cnt[N], colors;
        longs other;

        void init()
        {
            memset(cnt, 0, sizeof(cnt));
            memset(contrib, 0, sizeof(contrib));
            total = colors = 0;
        }

        dfs count = [](int u, int father)
        {
            size[u] = 1; bool zero = !(cnt[c[u]] ++);
            using namespace FWS;
            for (int ii = head[u]; ~ii; ii = ee[ii].next)
            {
                edge &e = ee[ii]; int &v = e.v;
                if (v == father || vis[v]) continue;
                count(v, u); size[u] += size[v];
            }
            if (zero)
            {
                total += size[u];
                contrib[c[u]] += size[u];
            }
            -- cnt[c[u]];
        };

        dfs disContrib = [](int u, int father)
        {
            bool zero = !(cnt[c[u]] ++);
            using namespace FWS;
            for (int ii = head[u]; ~ii; ii = ee[ii].next)
            {
                edge &e = ee[ii]; int &v = e.v;
                if (!vis[v] && v != father) disContrib(v, u);
            }
            if (zero)
            {
                total -= size[u];
                contrib[c[u]] -= size[u];
            }
            -- cnt[c[u]];
        };

        dfs reContrib = [](int u, int father)
        {
            bool zero = !(cnt[c[u]] ++);
            using namespace FWS;
            for (int ii = head[u]; ~ii; ii = ee[ii].next)
            {
                edge &e = ee[ii]; int &v = e.v;
                if (!vis[v] && v != father) reContrib(v, u);
            }
            if (zero)
            {
                total += size[u];
                contrib[c[u]] += size[u];
            }
            -- cnt[c[u]];
        };

        dfs update  = [](int u, int father)
        {
            bool zero = !(cnt[c[u]] ++);
            if (zero)
            {
                total -= contrib[c[u]];
                ++ colors;
            }
            sum[u] += total + colors * other;
            using namespace FWS;
            for (int ii = head[u]; ~ii; ii = ee[ii].next)
            {
                edge &e = ee[ii]; int &v = e.v;
                if (!vis[v] && v != father) update(v, u);
            }
            if (zero)
            {
                total += contrib[c[u]];
                -- colors;
            }
            -- cnt[c[u]];
        };

        dfs clear = [](int u, int father)
        {
            cnt[c[u]] = contrib[c[u]] = 0;
            using namespace FWS;
            for (int ii = head[u]; ~ii; ii = ee[ii].next)
            {
                edge &e = ee[ii]; int v = e.v;
                if (!vis[v] && v != father) clear(v, u);
            }
        };
    }

    auto cleanRoot = [](int size)
    {
        _root = 0; _part = inf;
        _sum = size;
    };

    auto setRoot = [](int u, int maxPart)
    {
        _part = maxPart;
        _root = u;
    };

    inline void init()
    {
        memset(vis, 0, sizeof(bool) * (n + 1));
        setRoot(0, inf); innerDFS::init();
    }

    int findRoot(int u, int father)
    {
        size[u] = 1; int maxPart = 0;
        using namespace FWS;
        for (int ii = head[u]; ~ii; ii = ee[ii].next)
        {
            edge& e = ee[ii]; int& v = e.v;
            if (v == father || vis[v]) continue;
            findRoot(v, u);
            size[u] += size[v];
            maxPart = max(maxPart, size[v]);
        }
        maxPart = max(maxPart, _sum - size[u]);
        if (maxPart < _part) setRoot(u, maxPart);
        return _root;
    }

    void calculate(int u)
    {
        using namespace innerDFS;
        using namespace FWS;
        count(u, 0);
        sum[u] += total - contrib[c[u]] + size[u];
        for (int ii = head[u]; ~ii; ii = ee[ii].next)
        {
            edge &e = ee[ii]; int v = e.v;
            if (vis[v]) continue;

            cnt[c[u]] = 1; total -= size[v];
            contrib[c[u]] -= size[v];
            disContrib(v, u);
            cnt[c[u]] = 0;

            other = size[u] - size[v];
            update(v, u);

            cnt[c[u]] = 1; total += size[v];
            contrib[c[u]] += size[v];
            reContrib(v, u);
            cnt[c[u]] = 0;
        }
        colors = total = 0; clear(u, 0);
    }

    void dc(int u)
    {
        vis[u] = true; calculate(u);
        using namespace FWS;
        for (int ii = head[u]; ~ii; ii = ee[ii].next)
        {
            edge &e = ee[ii]; int &v = e.v;
            if (vis[v]) continue;
            cleanRoot(size[v]);
            auto root = findRoot(v, u);
            dc(root);
        }
    }

    inline void solution()
    {
        init();
        cleanRoot(n);
        auto root = findRoot(1, 0);
        dc(root);
    }
}

int main()
{
    ios::sync_with_stdio(false);
    cin.tie(nullptr);

    cin >> n; FWS::init(); int x, y;
    for (int i = 1; i <= n; ++ i) cin >> c[i];
    for (int i = 1; i < n; ++ i)
    {
        cin >> x >> y;
        addEdge(x, y, 0);
    }
    PointDC::solution();
    for (int i = 1; i <= n; ++ i)
        cout << sum[i] << endl;

    return 0;
}

关于disContrib和reContrib：两个行为是对称的，你可以合成一个函数，也可以开一些全局变量记录这些修改；此外，这个题目还有 O(n) 的算法；想要了解可以去看这题的题解。

洛谷 P2305 [NOI2014]购票

这道题也相当的麻烦……

一颗有n个节点的有根树，所有的子节点向父节点连边；你可以从节点出发，支付这个节点的旅行费用，然后到达这个节点距离不超过 l 的祖先节点；每个节点有不同的 l 和费用：费用的计算方式是：f(dis) = dis*p + q；p和q是节点的常数。现要求求出从每个子节点出发到达根节点时的最少花费。

数据范围：N = 2e5，P = 1e6，Q = 1e12

总结&后记

参考资料

本篇博文在创作过程中参考了这些资料，在这里给出它们的链接：

如果觉得哪里没有说清楚你们也可以去看看这些链接。

博客内容遵循 署名-非商业性使用-相同方式共享 4.0 国际 (CC BY-NC-SA 4.0) 协议

本文永久链接是：https://shiraha.cn/2020/learn-point-dc-on-tree-and-dynamic-point-dc/

更新于：2020年4月23日

算法

ACM

学习笔记

评论