抱歉，您的浏览器无法访问本站

本页面需要浏览器支持（启用）JavaScript


了解详情 >

七つの海

今日、海を見た。もう怖くない

博客

随笔

朋友

归档

关于

Nowcoder 2020 暑期多校训练 （1）

七海

题解

发布于：2020年7月12日

次浏览

一共 10 个题目，能做的有几个？

听完叉姐（？）讲题目最速传说快于洛谷，好多题目都是论文的结论题…… 队内群友对此以及讲题纷纷发表各自的高见，可大佬的关注点总是和咱菜鸡不太一样…… 咱也不知道，咱也不敢问（

5KVYKS6_FJQEAQJGGX5.jpg
↑ 要被大一队友嫌弃力，乌乌 ↑

多亏这次是校队全队参加比赛，hls 已经开始撰写队内题解了，这是好的，不然我属实补不了题了（

A : B-Suffix Array

对于字符串 \(t_1t_2...t_k\)，有函数 \(B(t_1t_2...t_k) = b_1b_2...b_k\) 定义如下：

  • 若存在下标 j < i 使得 \(t_j = t_i\)，那 \(b_i = min_{1 \leq j \lt i, t_j = t_i} i - j\)；
  • 否则，\(b_i = 0\)；

对于给定长为 n 字符串 s 的 n 个后缀，根据 B 函数的值进行字典序排序；字符串 s 仅由 a 和 b 构成；

数据范围：n ≤ 1e5，Σn ≤ 1e6；

B : Infinite Tree

令 \(mindiv(n)\) 为 n 大于 1 的最小因数；现对于全体正整数，在 n - \(\frac n{mindiv(n)}\) 之间连边构成树；令 \(\delta (u,v)\) 为节点 u v 之间的边数，给定 \(w_1...w_n\)，求 \(min_u\sum^m_{i=1} w_i\delta(u,i!)\)。

数据范围：1 ≤ m ≤ 1e5，0 ≤ wi ≤ 1e4，Σm ≤ 1e6；

C : Domino

有两个 n × m 的矩阵，由 1 × 2 的砖块和 2 × 1 的砖块密铺；你可以将 2 × 2 范围内的两块相同的砖块调转方向（换成两块另一种砖块），问你需要操作多少次才能使得两个矩阵中的砖块排布一致；

数据范围：n, m ≤ 1e3，n × m ≤ 2e6；

D : Quadratic Form

太麻烦了……

E : Counting Spanning Trees

二分图包含 X（n个节点）和 Y（m个节点）两个部分；每一个 \(x_i\) 连接到了 Y 的前 \(a_i\) 个节点；给定 n, m, a 和 mod，求在模 mod 意义下生成树的数量；

数据范围：1 ≤ n,m ≤ 1e5，1 ≤ mod ≤ 1e9，1 ≤ a ≤ m，Σn ≤ 1e6；

F : Infinite String Comparision

s 为字符串，定义 \(s^\infty\) 为字符串 s 的无穷循环；现给定字符串 a, b，要求比较 \(a^\infty, b^\infty\)；

数据范围：1 ≤ |a|, |b| ≤ 1e5，Σs ≤ 1e6；

签到题，稍微优雅的暴力（直接比较）就可以过但是我白给两发；但是其实也是有正经做法的，原题解中说到：

通过 Periodicity Lemma，仅比较前 a + b - gcd(a, b) 个字符即可判断字符串大小；

所以，这个代码暴力的极限不是 LCM，而是定理中的 Periodicity Lemma；

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
#include <iostream>
#include <cstdio>
#include <cctype>
#include <algorithm>
#include <cstring>

using namespace std;
using longs = long long;
using uint = unsigned;

inline int nextInt()
{
    int x = 0, f = 1, ch = getchar();
    while (!isdigit(ch)) if (ch == '-') f = -1, ch = getchar();
    while (isdigit(ch)) x = x * 10 + ch - 48, ch = getchar();
    return x * f;
}

inline longs gcd(longs a, longs b)
{
    if (a < b) swap(a, b);
    if (!b) return a;
    else return gcd(b, a % b);
}

string a, b;

int main()
{
    ios::sync_with_stdio(false);
    std::cin.tie(nullptr);
    std::cout.tie(nullptr);

    while (cin >> a >> b)
        if (a.length() == b.length())
        {
            if (a == b) cout << '=' << endl;
            else if (a < b) cout << '<' << endl;
            else cout << '>' << endl;
        }
        else
        {
            longs _a = a.length(), _b = b.length();
            longs ca = 0, cb = 0, cnt = 0;
            longs lim = _a + _b - gcd(_a, _b);
            while (cnt < lim)
            {
                if (a[ca] != b[cb]) break;
                ca = (ca + 1) % _a;
                cb = (cb + 1) % _b;
                ++ cnt;
            }
            if (cnt == lim) cout << '=' << endl;
            else if (a[ca] < b[cb]) cout << '<' << endl;
            else cout << '>' << endl;
        }

    return 0;
}

那么什么是 Periodicity Lemma 呢？

关于 Periodicity Lemma

周期引理：字符串 S 有循环节 p 和 q 并满足 p + q ≤ |S| + gcd(p, q)，那么 gcd(p, q) 也是一个循环节；

在这一题里的用法？

显然，a 和 b 是待比较字符串（现设为 A 和 B，长度为 ∞）的循环节；我们先假设 A = B = S，那么 a 和 b 都是 S 的循环节；因为 |S| = ∞，所以 a + b - gcd(a, b) ≤ |S| 可以使用周期引理：gcd(a, b) 是 S 的循环节；因为串 gcd(a, b) 较短，它成为了循环节，则整个串显然相同；

如果 A，B 的前 a + b - gcd(a, b) 位不相同，则不能被看作是一个字符串，上述假设就失效了；这时也可以判定字符串的字典序大小，直接输出即可；

简单的说，若两个字符串相等的假设成立，那么就一定可以证明 gcd(a, b) 长度的字串是循环节，这个串的长度小于 a 和 b，且再使用引理的过程中已经判等了，所以两个串相等，假说也成立；

引理证明？

组内大佬证明了，我学会了再发上来；

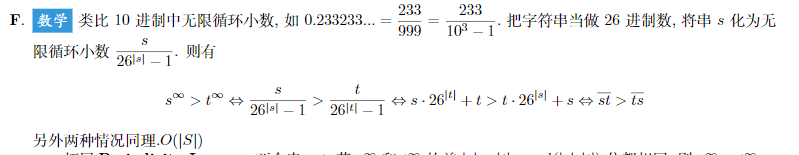
F-Lemma-hjl.png

先贴另一个组内大佬的证法 ↑

G : BaXianGuoHai, GeXianShenTong

太长了不翻译了……

H : Minimum-cost Flow

有一个网络，包括 n 个节点和 m 个弧边，每条边有费用 c；

进行 q 次询问，每个询问当所有边的容量为 u/v 时，将单位流量从节点 1 到节点 n 所需要的最小费用；

可行时，输出最小费用，否则输出 NaN；

数据范围：2 ≤ n ≤ 50，1 ≤ m ≤ 100，c, q ≤ 1e5，u, v ≤ 1e9；Σm ≤ 1e4，Σq ≤ 1e6；

I : 1 or 2

一张图，有 n 个点，给定 m 条边；问可不可以选出一些边，使得第 i 个点恰好连接了 \(d_i\) 条边；只需要判断是否可行，而无需输出具体选择方案。

数据规模：不超过 100 组测试数据；n ≤ 50，m ≤ 100，\(d_i \in\) {1, 2}；

J : Easy Integration

求 \(\int_0^1 (x - x^2)^n dx\) 在 998244353 下的模，n ≤ 1e6；不超过 1e5 组数据。

一个计算题，因为大一队友光速推出公式所以我就直接码代码了；没想到还是有点麻烦的……

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
#include <iostream>
#include <cstdio>
#include <cctype>
#include <algorithm>
#include <cstring>

using namespace std;
using longs = long long;
using uint = unsigned;

inline int nextInt()
{
    int x = 0, f = 1, ch = getchar();
    while (!isdigit(ch)) if (ch == '-') f = -1, ch = getchar();
    while (isdigit(ch)) x = x * 10 + ch - 48, ch = getchar();
    return x * f;
}

const longs mod = 998244353;
const longs p = mod - 2;

int fracMod(longs a, longs b)   // 费马小定理法
{
    auto n = p;
    longs ans = 1;
    while (n)
    {
        if (n & 1) ans = (ans * b) % mod;
        b = (b * b) % mod;
        n >>= 1;
    }
    ans = (ans * a) % mod;
    return (int) ans;
}

const int N = 1e6 + 5;
longs ans[N];

auto init = []
{
    longs a = 1, b = 1;
    for (longs i = 1; i < N; ++ i)
    {
        a = (a * i) % mod;
        b = (2 * b * (2 * i + 1)) % mod;
        ans[i] = fracMod(a, b);
    }
};

int main()
{
    ios::sync_with_stdio(false);
    std::cin.tie(nullptr);
    std::cout.tie(nullptr);

    init();
    longs n;
    while (cin >> n) cout << ans[n] << endl;

    return 0;
}

后记

博客内容遵循 署名-非商业性使用-相同方式共享 4.0 国际 (CC BY-NC-SA 4.0) 协议

本文永久链接是：https://shiraha.cn/2020/nowcoder-2020-summer-multi-1/

更新于：2020年7月12日

算法

ACM

Nowcoder

评论