比赛赛题地址:https://ac.nowcoder.com/acm/contest/4462 按照惯例,开始之前先码了官方题解:https://ac.nowcoder.com/discuss/369662
 TIM图片20200226090513.jpg
TIM图片20200226090513.jpg怎么说呢,虽然做题目的情况也并没有多少的改善,但是这次确实就是div3水平== 好多题目都是暴力求解的,姑且在这里简单的提一下,算是一个总结吧。毕竟只有比赛途中自己做出来的题目才算的上是真正会的==
题解
A - 操作序列
题目地址:https://ac.nowcoder.com/acm/contest/4462/A
看讨论帖子中五花乱坠的平衡树啊、线段树啊……什么的,我只觉得他们吵闹——这个题目并没有涉及到任何的区间变动,完全可以直接STL的map怼上去。只是要注意一点,查询一个不存在的元素会导致它被新建,所以查完了还得把它删掉,不然就比较麻烦。
官方题解提示了平衡树在线,但是它自己也是拿set做的,和我用map并没有什么本质的区别/// 唯一值得一提的就是读入的时候,因为cin在读取的时候不会自动略过换行符什么的,所以一开始getline容易读到空行。可以直接用循环跳过读入的空行即可。
B - 树上子链
题目地址:https://ac.nowcoder.com/acm/contest/4462/B
还算是比较简单的递推关系,题解说这算是DP那就算吧。大概就是每个节点都要查询一次,然后更新一次答案并返回一个最长链供父亲使用的感觉。官方题解说的dp[i]就是要返回的以i节点为根的最长子链,最大值官方题解也是维护了最大和次大的长链求和的,没啥好说的。
题解大多说这是一个求“树的直径”的问题,是一个没有听说过的名词,所以在这里介绍一下这个定义:
树的直径:我们将一棵树 T = ( V,E ) 的直径定义为 maxδ ( u,v ),其中 u,v ∈ V。也就是说,树中所有最短路径距离的最大值即为树的直径。
一般这种题目给的是边长,但是这个题目给的是点权,因此做法有略微的差别。经典的求树的直径的做法有两种:BFS/DFS和树形DP。先码一个例题在这里:POJ 1985。
搜索方法:先从任意一点P出发,找离它最远的点Q,再从点Q出发,找离它最远的点W,W到Q的距离就是树的直径。正确性的证明可以看下方的引用:
原作者: forever_dreams 来源: https://blog.csdn.net/forever_dreams/article/details/81051578
搜索方法的正确性证明:
① 若P已经在直径上,根据树的直径的定义可知Q也在直径上且为直径的一个端点
② 若P不在直径上,我们用反证法,假设此时WQ不是直径,AB是直径:
若AB与PQ有交点C,由于P到Q最远,那么PC+CQ>PC+CA,所以CQ>CA,易得CQ+CB>CA+CB,即CQ+CB>AB,与AB是直径矛盾,不成立,如下图(其中AB,PQ不一定是直线,画成直线是为了方便):
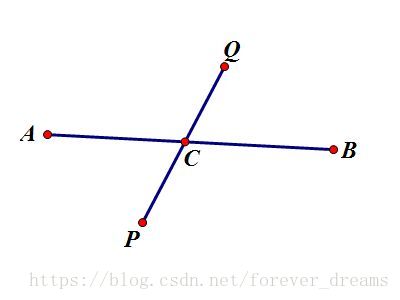 20180715124201842.jpg
20180715124201842.jpg若AB与PQ没有交点,M为AB上任意一点,N为PQ上任意一点。首先还是NP+NQ>NQ+MN+MB,同时减掉NQ,得NP>MN+MB,易知NP+MN>MB,所以NP+MN+MA>MB+MA,即NP+MN+MA>AB,与AB是直径矛盾,所以这种情况也不成立,如下图:
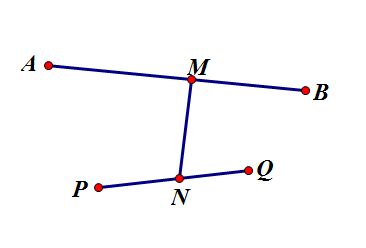 20180715145337618.jpg
20180715145337618.jpg
上面的证明排除了可能失败的两种情况,反证了做法的正确性。无论是上述的哪一种情况,都不能确定除了WQ之外的任意直径AB的存在,因此找到的WQ必然是直径。
树形DP方法:也就是这个题目推荐的做法,每个节点i维护两个值。一个是以i为根的子树中,i到叶子节点的最长链的长度;另一个是同样的条件下,这个长度的次大值。我们将它们记为dp1和dp2数组。
然后这个值是可以由下而上的推导的,设j是i的儿子,两节点之间路径的长度w[i][j];具体更新策略是:
- 若 dp1 [ i ] < dp1 [ j ] + w [ i ][ j ],先更新 dp2 [ i ] = dp1 [ i ],再更新 dp1 [ i ] = dp1 [ j ] + w [ i ][ j ];
- 否则,若 dp2 [ i ] < dp1 [ j ] + w [ i ][ j ],直接更新 dp2 [ i ] = dp1 [ j ] + w [ i ][ j ];
这是很容易理解的:首先假定最长链和次长链和此节点构成了直径,更新最大值;然后再将最大值向上传递。最后的答案就是 ans = max(dp1[i]+dp2[i])。
C - 交换游戏
题目地址:https://ac.nowcoder.com/acm/contest/4462/C
真就暴力搜索呗()预处理所有的情况随便DFS可也太顶了== 不过反正字符串就长度只有12,确实可以为所欲为()
D - 收集纸片
题目地址:https://ac.nowcoder.com/acm/contest/4462/D
10张纸片,不同的顺序也没多少种情况,还是一个因为范围不大所以可以为所欲为的题目。出题人说了,全排列然后找最小值也是能过的,但是也有一些还算是算法的做法:就是使用状压DP的方法的旅行商问题的解法。
这代码事后补的,直接看还是有点混乱的:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
| #include <iostream>
#include <cmath>
#include <cstdlib>
#include <algorithm>
#include <cstring>
#define rint register int
using namespace std;
typedef long long longs;
typedef long double longd;
const char mod[] = "The shortest path has length ";
struct coord
{
int x,y;
int operator-(const coord& c);
};
int t,N,M,n;
coord st,pp[20];
int dis[20][20];
int dp[1<<11][20];
int main()
{
ios::sync_with_stdio(false);
cin.tie(nullptr);
while(cin>>t) while(t--)
{
cin>>N>>M>>st.x>>st.y;
cin>>n;
pp[0] = st;
for(int i=1;i<=n;++i)
cin>>pp[i].x>>pp[i].y;
for(int i=0;i<=n;++i)
for(int j=i;j<=n;++j)
dis[i][j]=dis[j][i]=pp[i]-pp[j];
memset(dp,0x3f,sizeof(dp));
const int lim = (1<<n+1)-1;
dp[0][0] = dp[1][0] = 0;
for(rint i=1;i<=lim;++i)
for(int j=0;j<=n;++j)
if(i>>j&1)
for(int k=0;k<=n;++k)
if(i>>k&1)
dp[i][j]=min(dp[i][j],dp[i^(1<<j)][k]+dis[k][j]);
int ans = 0x7fffffff;
for(int i=1;i<=n;++i)
ans = min(ans,dp[lim][i]+dis[i][0]);
cout<<mod<<ans<<endl;
}
return 0;
}
int coord::operator-(const coord& c)
{
return abs(x-c.x)+abs(y-c.y);
}
|
G - 仓库选址
题目地址:https://ac.nowcoder.com/acm/contest/4462/G
温馨提示: 本题的C++时间限制是4s
本来还看着是一个非常奇怪的题目,但是给了4s的话就完全可以暴搜了== 当然也可以做一些力所能及的但是没啥x用的优化:比如记录二维前缀和,用贡献差来替换多次的暴搜;也可以利用直观感受,直接查找中位数进行检查。
所有数与中位数的绝对差之和最小。
这里的代码就是查找中位数的版本:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
| #include <iostream>
#include <cstring>
#include <utility>
using namespace std;
typedef long long longs;
typedef long double longd;
int mat[105][105];
longs row[105],col[105];
longs res = 0;
pair<int,int> midium(int n,int m)
{
const longs half = res+1>>1;
longs tmp; int i,j;
for(i=1,tmp=0;i<=m,tmp<half;++i)
tmp += row[i];
for(j=0,tmp=0;j<=n,tmp<half;++j)
tmp += col[j];
return make_pair(--i,--j);
}
int main()
{
ios::sync_with_stdio(false);
cin.tie(nullptr);
int T,n,m;
while(cin>>T)while(T--)
{
cin>>n>>m;
res = 0;
memset(row,0,sizeof(row));
memset(col,0,sizeof(col));
for(int i=1;i<=m;++i)
for(int j=1;j<=n;++j)
{
cin>>mat[i][j];
row[i]+=mat[i][j];
col[j]+=mat[i][j];
res+=mat[i][j];
}
auto mid = midium(n,m);
int &x = mid.first, &y = mid.second;
longs out = 0;
for(int i=1;i<=m;++i)
for(int j=1;j<=n;++j)
out += mat[i][j]*(abs(i-x)+abs(j-y));
cout<<out<<endl;
}
return 0;
}
|
总感觉这题目给人一种既视感,但是又不是很清楚…… 之所以能利用中位数的原因是题目采用的是曼哈顿距离吧。如果距离采用的是直线连接的小数距离的话,这个题目还可以利用中位数来解决吗?曼哈顿距离和直线距离可不是一回事了(
H - 货物种类
题目地址:https://ac.nowcoder.com/acm/contest/4462/H
题目说区间修改,那就是说要维护一个差分序列;区间操作,只在最后有一次询问,询问少,大概是要用线段树的。一开始以为不能用树状数组,后来寻思了一下应该还是可以用的,只是不能维护max值,需要一次遍历来找出最大值就是了()。
但是线段树还是太麻烦了,所以还是直接维护差分数组算了。此处吐槽一下题解的代码,有点小乱()
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
| #include <iostream>
#include <map>
#include <vector>
using namespace std;
typedef long long longs;
typedef long double longd;
const int N = 1e5+10;
int main()
{
ios::sync_with_stdio(false);
cin.tie(nullptr);
int n,m,l,r,d;
while(cin>>n>>m)
{
vector<int> mount[N];
vector<int> umount[N];
map<int,int> mounted;
while(m--)
{
cin>>l>>r>>d;
mount[l].push_back(d);
umount[r].push_back(d);
}
int now = 0, max = -1, pos = 1;
for(int i=1;i<=n;++i)
{
for(int j : mount[i])
{
if(!mounted[j])++now;
++mounted[j];
}
if(now>max)
{
max = now;
pos = i;
}
for(int j : umount[i])
{
--mounted[j];
if(!mounted[j])--now;
}
}
cout<<pos<<endl;
}
return 0;
}
|
第一次自己写的时候是寻思着合并区间的,然后一次给加上去,再根据差分求出最大值,但是不知道因为什么原因最后WA了…… 于是就因为各种原因懒得一行一行看自己的代码,不再合并区间重新写了一遍,就A了。
再感慨一下,这map用来当JavaScript中的无限大的稀疏数组实在是太舒服了()
I - 工具人
题目地址:https://ac.nowcoder.com/acm/contest/4462/I
这题大概就是这次比赛中的毒瘤题吧?明显要用到浮点运算,然后还是一个看起来就很乱的模型…… 整个比赛中途只有个位数的人A了这个题,截止我补题,我才是第十个A了这个题目的人()
要说做法倒也毫无新意,就是贪心。不过这次不是光线的距离——这也没法算,而是巧妙地将这个随着距离变化而权重变化的距离变成了到原点的角度范围,然后利用角度范围作为贪心区间。这种贪心的结果显然是确定了起点就确定了,可能会考虑不到跨边界的联合,所以为了保证每一种情况都被考虑到,切换起点进行贪心取最小值就可以做出来。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
| #include <iostream>
#include <cmath>
#include <algorithm>
#include <vector>
using namespace std;
typedef long long longs;
typedef long double longd;
enum bound {st=0,ed=1};
const double EPS = 1e-8;
const double PI = 3.1415926535897932384626;
const double PI2 = 2*PI;
struct ray
{
int num;
double angle;
bound type;
ray(int n,double ag,bound typ);
bool operator<(const ray &r) const;
bool operator<(const ray &&r) const;
};
int main()
{
ios::sync_with_stdio(false);
cin.tie(nullptr);
int t,n,d,x,y;
int cnt;
while(cin>>t) while(t--)
{
cin>>n>>d;
vector<ray> v;
longs d2 = d*d;
longd r2;
cnt = 0;
for(int i=1;i<=n;++i)
{
cin>>x>>y;
r2 = x*x+y*y;
if(r2-EPS <= d2) continue;
longd angle = atan2(y,x);
longd delta = asin(d/sqrt(r2));
++cnt;
v.emplace_back(cnt,angle-delta,st);
v.emplace_back(cnt,angle+delta,ed);
}
if(!cnt)
{
cout<<1<<endl;
continue;
}
sort(v.begin(),v.end());
int vs = v.size();
int ans = cnt;
for(int i=0;i<vs;++i)
{
vector<bool> mark(cnt+1,false);
vector<int> list;
int c = 0;
for(int j=0;j<vs;++j)
{
auto &vj = v[(i+j)%vs];
if(!vj.type)
{
mark[vj.num] = true;
list.push_back(vj.num);
}
else if(mark[vj.num])
{
++c;
for(auto li : list)
mark[li] = false;
list.clear();
}
}
c += list.size();
if(c<ans) ans = c;
}
cout<<ans<<endl;
}
return 0;
}
bool ray::operator<(const ray &r) const
{
if(fabs(angle-r.angle)>EPS)
return angle < r.angle;
return type < r.type;
}
bool ray::operator<(const ray &&r) const
{
return *this < r;
}
ray::ray(int n, double ag, bound typ)
{
num = n;
type = typ;
angle = fmod(ag+PI2,PI2);
}
|
关键就在于想到将距离变成角度。也许……起到了开拓思维的作用?第一次写的时候使用不太熟练的C++简化构造器炸了,所以写代码还是少搞这些没用的东西==
签到题
本次的签到题是E题、F题和J题。特别要注意的是J要手打高精度,应当注意细节。
后记
怎么说呢,不是暴力就是简单题。但是做题的那个状态下还真就不一定能做的出来== I题算是一个比较有点思维的题目,代码实现也应当更加谨慎。很多题目还是要多参考参考数据范围,万一暴搜行呢(捂脸)
参考链接
树的直径部分:https://blog.csdn.net/forever_dreams/article/details/81051578










